Stable Distribution with Minimal Information
Despite the abundance of normal distributions in the finance literature (e.g. Geometric Brownian motion) during my time doing finance research I have come to the realization that 9 out of 10 of the various quantities that I study follow a fat-tailed distribution that lies somewhere between Cauchy and Gaussian, rather than a Gaussian.
I feel there must be a deeper reason beyond mere coincidence. I present here an informal argument why I think that is the case.
Fundamentally the financial market is a game of information. Any consistently profitable strategy is, on the deepest level, a form of information arbitrage - you know something that your counterparties or other market participants don’t. Unfortunately every time you act on such information you are also leaking it out to the market. For example let’s say your proprietary model predicts that TSLA stock is going up tomorrow, so you decided to buy 10,000 TSLA stocks based on this information. By doing so you are also broadcasting your prediction to the whole market, which will react by raising the price. Through this process the market effectively ingested and incorporated your proprietary information, and now you no longer has the informational edge.
In a highly competitive market it is important to minimize this informational leakage. If all market participants do their best to hide their information then the distribution of any tradeable quantity would satisfy some minimal information criteria. Tradeable quantities are not limited to prices, but essentially anything that a trading strategy can react to, and by reacting to it would also affect its value.
So how do we formulate such a minimal information criteria? We need to answer two questions - what do we consider to be the search space of allowable distribution, and how do we measure the information content of a distribution. For the first question we shall limit ourselves to (Lévy-)stable distributions because the collective effect of a large number of market participates should lead to some form of large-number effect (Generalized Central-Limit Theorem). For the second question we use the notion of Fisher information (physicist’s information).
Below are plots of stable distributions with the same scale parameter of one and all centered around zero. The parameter \(\alpha\) controls the shape of the distribution with the normal distribution having \(\alpha=2\) and the Cauchy distribution having \(\alpha=1\):
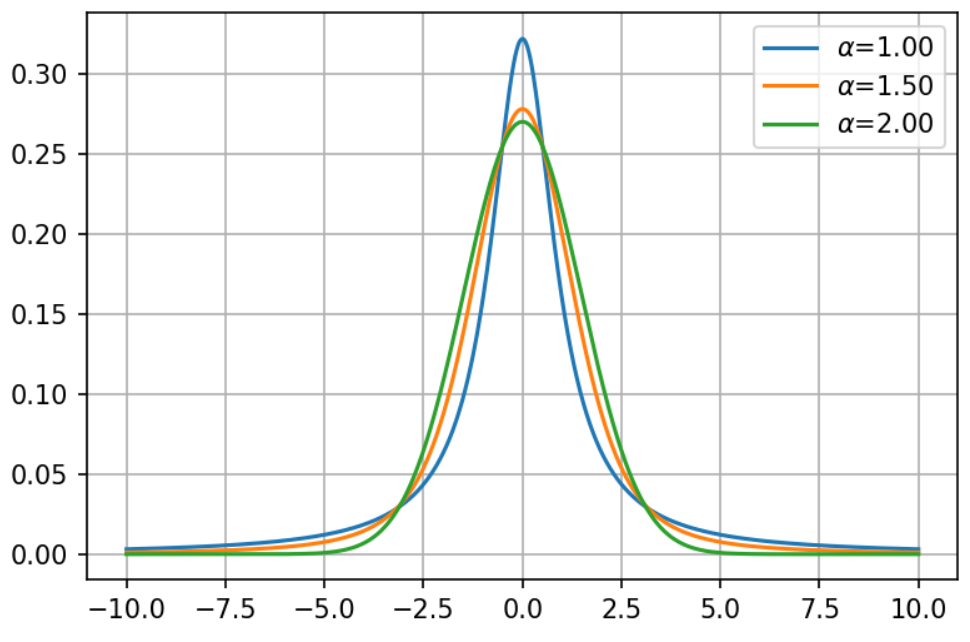
For each \(\alpha\) we can calculate the Fisher information of the distribution. We can see that the minimum occurs somewhere around 1.4-1.5:
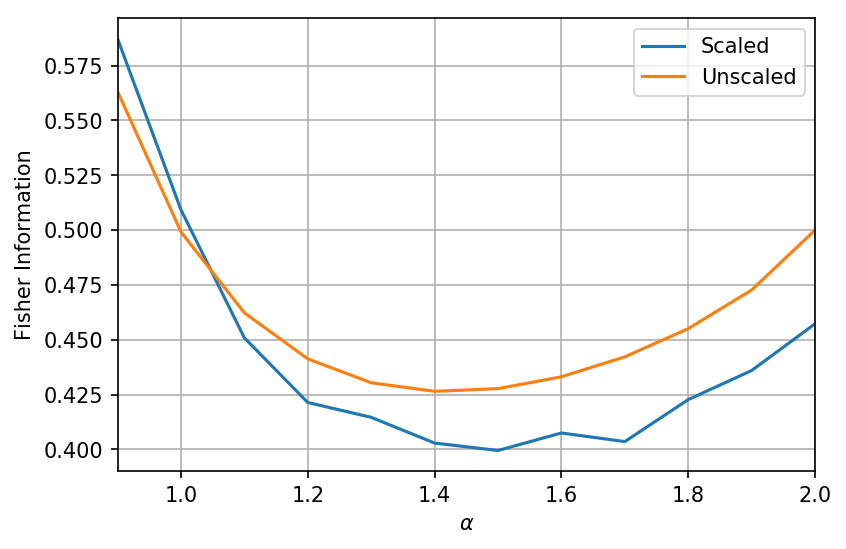
The difference between scaled and unscaled is the distributions in the scaled family are scaled to all have the same median absolute deviation of 1 while the unscaled family simply all have the same scale parameter of 1.
I believe the above plot is the reason behind the fact that a lot of distributions in finance seems to be significantly more tailed than Gaussian but not as heavily-tailed as Cauchy. In fact I’d like to propose standardizing the \(\alpha\)-1.5 stable distribution as the default distribution in market structure research.
