Preserving Curvature while Smoothing via Anisotropic Diffusion

When handling noisy data we often apply some form of rolling averages or kernel smoothing techniques to remove the high-frequency noise from the data. These simple techniques are easy to use and often produce good enough results. However one big draw-back of this kind of simple local-averaging techniques is that they also dampen the curvature that is contained in the original data:

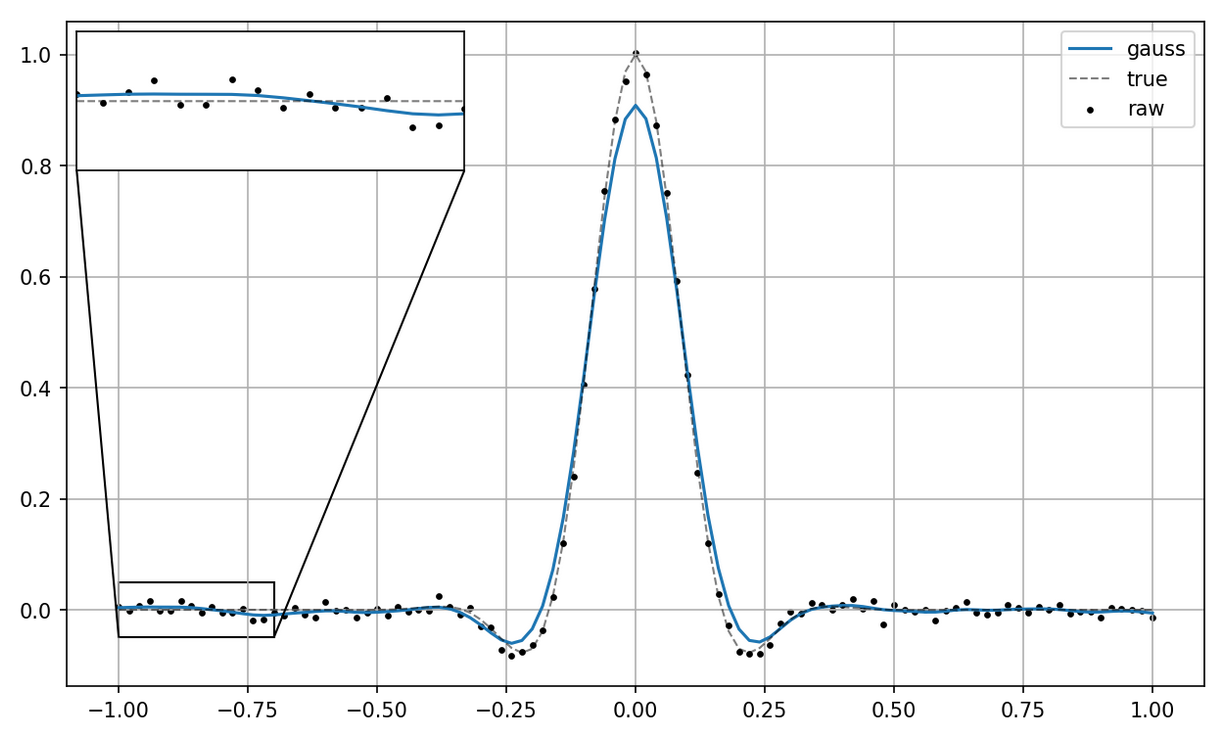
We can see that the height of the central peak is significantly reduced, due to this curvature-dampening effect.

In a scenario where the curvature contains important information, this behavior is highly detrimental. Fortunately there exists a curvature-preserving smoothing technique called anisotropic diffusion which essentially adjusts the width of the smoothing kernel in response to the estimated local curvature, thus preserving the curvature in the original data:

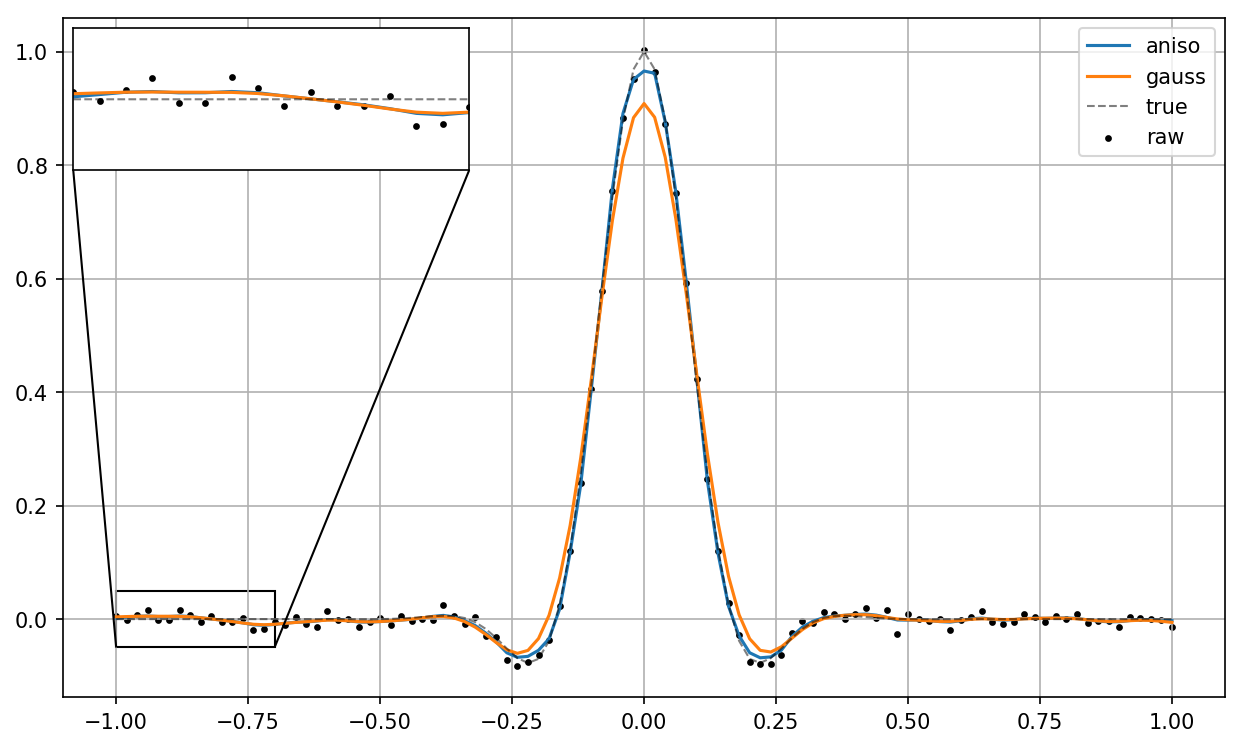
The algorithm is relatively simple to implement (see for example this implementation). However it requires a bit of tuning due to having more hyperparameters, and thus is not as simple to use as e.g. the usual Gaussian smoothing.