As Large Language Models (LLMs) get better at complex reasoning, we need better ways to measure the difficulty of the tasks we give them. A fascinating paper from researchers at Apple, “The Illusion of Thinking”, systematically tested models like Claude 3.7 Sonnet on various puzzles. They measured complexity using straightforward metrics like the problem size ($n$) or the number of moves in the solution.

Their findings revealed an interesting inconsistency: models could solve a Tower of Hanoi puzzle requiring over 100 moves, yet fail on a River Crossing puzzle that needs only a dozen. This suggests that simple metrics like “number of moves” don’t provide a universal measure of difficulty. Different puzzles stress a model’s capabilities in different ways.

This post introduces a framework to normalize the concept of task difficulty into a single, unified metric: Cognitive Load ($\mathcal{L}$). By defining difficulty in terms of the underlying computational work a model must perform, we can explain why some seemingly simple problems are incredibly hard for LLMs and predict when their performance will start to degrade.

A Look at the Puzzles

To understand how cognitive load is calculated, it helps to first understand the mechanics of the puzzles used as benchmarks.

Tower of Hanoi

This puzzle features three pegs and $n$ disks of different sizes stacked on the first peg in size order (largest at bottom). The goal is to transfer all disks from the first peg to the third peg. Valid moves include moving only one disk at a time, taking only the top disk from a peg, and never placing a larger disk on top of a smaller one. The difficulty can be controlled by the number of initial disks; the minimum number of required moves with $n$ disks is $2^n - 1$.

Checker Jumping

This is a one-dimensional puzzle with red checkers, blue checkers, and a single empty space in a line. The objective is to swap the positions of all red and blue checkers, mirroring the initial configuration. Valid moves include sliding a checker into an adjacent empty space or jumping over exactly one checker of the opposite color to land in an empty space. Checkers cannot move backward. The complexity is controlled by the number of checkers: with $2n$ checkers (n of each color), the minimum number of moves is $(n + 1)^2 - 1$.

River Crossing

This is a constraint satisfaction puzzle involving $n$ “actors” and their corresponding $n$ “agents” who must cross a river in a boat. The goal is to transport all $2n$ individuals from one bank to the other. The boat has a limited capacity ($k$) and cannot travel empty. The core constraint is that an actor cannot be in the presence of another’s agent unless their own agent is also present. For $n=2$ and n=3, the boat capacity is $k=2$, and for larger $n$, $k=3$.

Blocks World

This block-stacking puzzle requires rearranging blocks from an initial configuration to a specified goal state. The objective is to find the minimum number of moves. Valid moves are restricted to the topmost block of any stack, which can be placed either on an empty space to start a new stack or on top of another block. The complexity is controlled by the number of blocks. While part of the original study, this puzzle was excluded from our main analysis due to its stochastic nature, which introduces significant noise into the performance data.

The Cognitive Load Framework

To create a single, unified metric for reasoning difficulty, we must start from a fundamental principle of computational work. The “true” cognitive load of a task is the sum of the work done at every deliberative step of its solution. The work at each step depends on the complexity of the rules being applied ($C$) and the size of the state information ($S_i$) relevant at that specific step.

$$W_{\text{total}} \approx C \times \sum_{i=1}^{N_{\text{steps}}} S_i$$

While this summation represents the ground truth, it can be unnecessarily complex to calculate. We therefore propose a more practical and operational model that approximates this work:

$$\mathcal{L}(I) = S_{\text{max}}(I) \times C(P) \times D(I)$$

In this formula, $S_{\text{max}}$ is the peak state complexity encountered, $C$ is the constant constraint complexity, and $D$ is a scaling factor that characterizes the structure of the algorithm’s solution path. The power of this model is that it generalizes well across different types of algorithms, as we will now show.

The Three Components of the Model

1. State Information Density ($S_{\text{max}}$)

This component quantifies the maximum working memory required at any single point during the problem-solving process.

Definition: The State Information Density, $S_{\text{max}}(I)$, is the Shannon entropy of the largest state space the model must consider to execute its algorithm for instance $I$.

2. Constraint Complexity ($C$)

This component quantifies the complexity of the puzzle’s ruleset.

Definition: The Constraint Complexity, $C(P)$, is the number of fundamental, atomic logical or relational predicates required to express the algorithm that validates a single move.

3. Solution Path Complexity ($D$)

This is a structural scaling factor that depends on the class of algorithm used to solve the puzzle. It accounts for how the state information changes over the course of the solution.

Case A: Iterative Algorithms

• Examples: River Crossing, Checker Jumping.
• Method: These problems are solved by exploring a state-space graph one step at a time. The relevant state information, $S_i$, is constant throughout this search and is equal to $S_{\text{max}}$.
• Justification: The true work sum becomes $C \times \sum S_{\text{max}} = C \times S_{\text{max}} \times N_{\text{steps}}$. Our model, $L = S_{\text{max}} \times C \times D$, is therefore an exact representation if we define $D$ as the number of steps in the solution path.
• Calculation of $D$: $D$ is the length of the shortest known solution path, $m(n)$.

Case B: Recursive Algorithms

• Example: Tower of Hanoi.
• Method: These problems are solved by breaking them down into smaller sub-problems. The state information the model must focus on, $S_i$, is smaller for the sub-problems than for the main problem. The “true work” sum resolves to be proportional to $C \times n^2$.
• Justification: Our model uses $S_{\text{max}}$ (the state of the full n-disk problem) and a scaling factor $D$. For $L = S_{\text{max}} \times C \times D$ to match the true $n^2$ scaling, $D$ must be proportional to $n$. This corresponds perfectly to the algorithm’s recursion depth. Our model is thus a well-justified approximation that correctly captures the problem’s scaling behavior.
• Calculation of $D$: $D$ is the maximum recursion depth of the algorithm.

The Cognitive Load Formula

The final formula provides a concrete method for calculating a single, unified difficulty score for any discrete reasoning task.

$$\mathcal{L}(I) = S_{\text{max}}(I) \times C(P) \times D(I)$$

Case Studies: The Framework in Action

Let’s apply this formula to the three puzzles mentioned earlier to see how it works in practice.

Case Study 1: Tower of Hanoi

• State ($S$): For $n$ disks and 3 pegs, there are $3^n$ configurations.

  $$S_{\text{hanoi}}(n) = \log_2(3^n) = n \log_2(3) \approx 1.58n$$

• Constraints ($C$): A move is valid if: 1) the source disk is the top of its peg, AND 2) the destination peg is either empty OR its top disk is larger. This requires 3 atomic predicates.

  $$C_{\text{hanoi}} = 3$$

• Path ($D$): The solution is recursive, and the number of cognitive steps corresponds to the recursion depth.

  $$D_{\text{hanoi}}(n) = n$$

• Cognitive Load ($\mathcal{L}$):

  $$\mathcal{L}_{\text{hanoi}}(n) = S(n) \times C \times D(n) = (1.58n) \times 3 \times n = 4.74n^2$$

Case Study 2: Checker Jumping

• State ($S$): The number of states for $2n+1$ squares grows such that the log-information is approximately $2n$.

  $$S_{\text{checkers}}(n) \approx 2n$$

• Constraints ($C$): The rules for valid moves (slides, jumps, directionality) are complex, requiring approximately 8 atomic predicates to define.

  $$C_{\text{checkers}} = 8$$

• Path ($D$): The puzzle requires planning to avoid dead ends, with a cognitive path length proportional to the minimum solution length.

  $$D_{\text{checkers}}(n) = n^2 + 2n$$

• Cognitive Load ($\mathcal{L}$):

  $$\mathcal{L}_{\text{checkers}}(n) \approx (2n) \times 8 \times (n^2 + 2n) = 16n^3 + 32n^2$$

Case Study 3: River Crossing

• State ($S$): With $n$ pairs of agents, the state is defined by the location of $2n$ individuals and the boat.

  $$S_{\text{river}}(n) = \log_2(2 \cdot 2^{2n}) = 2n + 1$$

• Constraints ($C$): The safety condition must be checked for all actors on both banks, which involves checking pairs of actors. The complexity grows quadratically.

  $$C_{\text{river}}(n) \approx 2n(n-1) = 2n^2 - 2n$$

• Path ($D$): Solving requires a state-space search, and the path length is the number of steps in the shortest solution, $m(n)$.

  $$D_{\text{river}}(n) = m(n)$$

• Cognitive Load ($\mathcal{L}$):

  $$\mathcal{L}_{\text{river}}(n) \approx (2n+1) (2n^2 - 2n) m(n)$$

Unified Performance Curve

The Apple paper provides accuracy data for Claude 3.7 Sonnet across these puzzles. When we re-analyze their data, not against problem size $n$ but against our calculated Cognitive Load, something remarkable happens. The performance data from all these different puzzles, which looked inconsistent before, now collapses onto a single, predictable curve.

By fitting a single sigmoid function (which describes a sharp transition) to the combined data from both puzzles, we can identify a unified critical threshold. The fit gives a consistent critical load of $\mathcal{L}_{\text{crit}} \approx 254$.

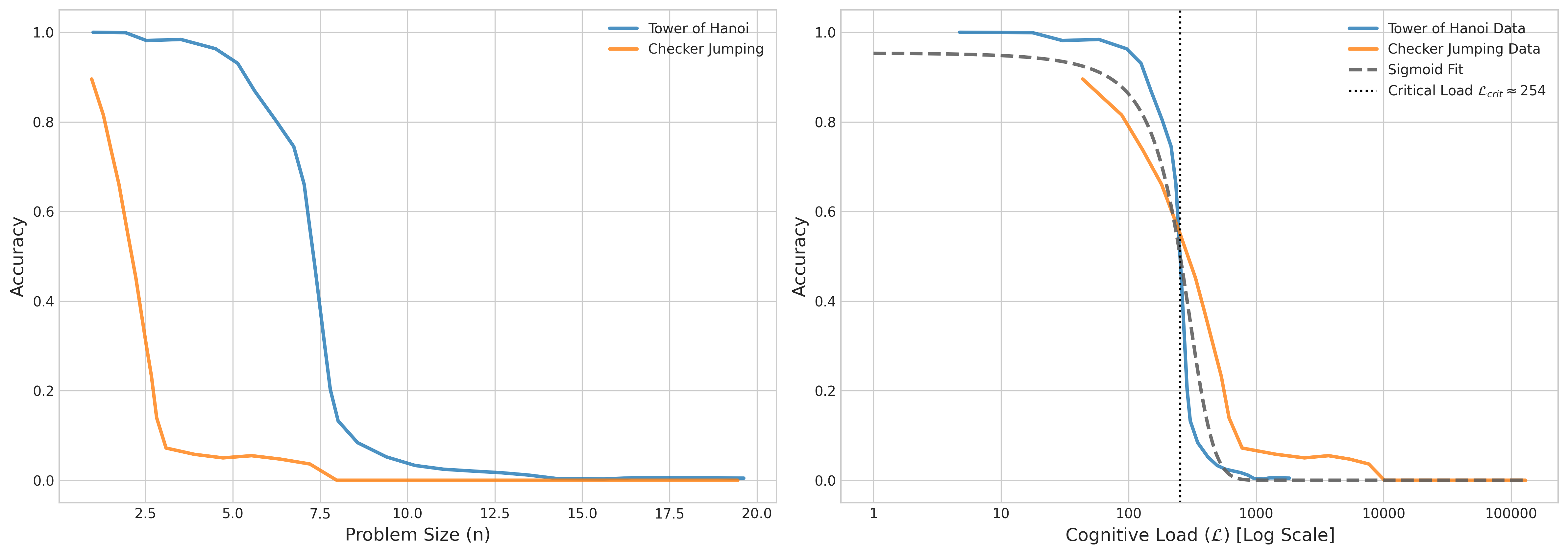Figure 1: Side-by-side comparison of Claude 3.7 Sonnet’s performance. Left: Plotting accuracy against problem size $n$ shows two completely different performance curves. Right: Plotting accuracy against the unified Cognitive Load ($\mathcal{L}$) metric aligns the data from both puzzles onto a single curve. The grey dashed line shows a single sigmoid curve fitted to all data points, revealing a consistent critical threshold of ~254.

This curve reveals a unified critical load threshold ($\mathcal{L}_{\text{crit}}$) for the model. Based on our analysis of the published data, this threshold for Claude 3.7 Sonnet appears to be around $\mathcal{L}_{\text{crit}} \approx 254$.

This threshold acts as a fundamental constraint on the model’s reasoning capacity.

Predicting Performance: A River Crossing Case Study

The true power of this framework lies not just in explaining performance but in predicting it. We can test this by applying the Cognitive Load formula to the River Crossing problem. The Apple paper reports a sharp performance drop for Claude 3.7 Sonnet on this specific puzzle: from ~80% accuracy for the $n=2$ case down to 0% for $n=3$. Let’s see if our model predicts this cliff.

• Case 1: River Crossing with n=2 (2 pairs, optimal solution has 5 moves)
  • Cognitive Load: $\mathcal{L}_{\text{river}}(2) \approx (2 \cdot 2 + 1)(2 \cdot 2^2 - 2 \cdot 2) \times 5 = 5 \times 4 \times 5 = 100$
  • This load is well below the critical threshold of ~254, correctly predicting a high likelihood of success.
• Case 2: River Crossing with n=3 (3 pairs, optimal solution has 11 moves)
  • Cognitive Load: $\mathcal{L}_{\text{river}}(3) \approx (2 \cdot 3 + 1)(2 \cdot 3^2 - 2 \cdot 3) \times 11 = 7 \times 12 \times 11 = 924$
  • This load is nearly four times the critical threshold, correctly predicting catastrophic failure.

The framework’s predictions align perfectly with the observed results. The model succeeds when the task is below its cognitive limit and fails when the task exceeds it. This demonstrates how Cognitive Load provides a more robust and predictive measure of task difficulty than simple metrics like the number of moves. This also helps explain the paper’s finding that models’ reasoning effort (measured in token usage) declines at high complexity; once the cognitive load is past the critical threshold, the model effectively gives up.

Conclusion

The Cognitive Load framework provides a structured way to think about and quantify the difficulty of reasoning tasks for LLMs. By breaking down the problem into State, Constraint, and Path complexity, we get a metric that is both theoretically sound and seems to work in practice when applied to existing research data.